Quick Start

How to set up an ODE

How to set up an OCP: Quick Start for Beginners

In this section an incremental set of examples for preparing an OCP is presented. The first example is the classic bang-bang mass, the basic instructions for a quick start are introduced. The next examples will add more and more features in order to give a sufficiently deep insight in PINS. For a more detailed description, refer to the next chapters where the single commands of XOptima are listed.

Example 1: Fixed Time Bang Bang

In PINS each problem must have a name, for this first tutorial choose for simplicity “Fixed_Time_Bang_Bang”. The best thing to do is to create on a desired location the folder Fixed_Time_Bang_Bang and the subfolder model. Inside that subfolder create an open a Maple© worksheet called Fixed-Time-Bang-Bang.mw, this will contain all the necessary instruction for XOptima to define the OCP and generate the optimised C++ code for Mechatronix ToolKit that will be run by PINS. The situation in your folder should be the one depicted in initial folder tree.

Attention

Initial folder tree

The folder tree for the first start with PINS

•   Fixed_Time_Bang_Bang

•   model

•   Fixed_Time_Bang_Bang.mw

You are now ready to define the OCP! Suppose to solve the following OCP: maximise [1] the distance of a classic bang-bang mass starting at the origin and standing at rest at the final point. The time interval is fixed in \([0,T]\) with \(T=1\). The equations of the problem are:

(1)\[\begin{align*} \textrm{minimize:}\quad & \int_0^T -v(t)\dt = -x(T) \\[1em] \textrm{subject to}\quad & x'(t)=v(t), \quad v'(t)=u(t), \qquad t\in[0,1]\\[1em] & x(0)=0, v(0)=0, v(T)=0; \qquad u(t)\in [-2,1]. \end{align*}\]

The first thing to do in Maple© is to load the XOptima Library with the command

with(XOptima):

Module '     XOptima', Copyright (C) B-cube Team ...
Module ' XOptimaPars', Copyright (C) B-cube Team ...
Module ' XOptimaSUBS', Copyright (C) B-cube Team ...

This will display information of the version of XOptima and the credits, of course now you have loaded the package. The next step is to define the states and controls. The corresponding variables are \(x(t)\), \(v(t)\) - position and velocity - and \(u(t)\) the control.

qvars := [x(t),v(t)];
cvars := [u(t)];

Having defined the variables, it is possible to define the dynamical system by specifying the differential equations:

EQ1 := diff(x(t),t) = v(t);
EQ2 := diff(v(t),t) = u(t);

With the next instruction the dynamical system is given to XOptima:

loadDynamicSystem( equations = [EQ1,EQ2],
                   controls  =  cvars,
                   states    =  qvars);

This instruction will output the message “Independent variable \(t\) has been redefined to ‘zeta’” and the confirm of the state variables in \(\zeta\). Now you can select which boundary conditions are active, in this case the initial conditions f or \(x\) and \(v\) and the final condition on \(v\), then you can specify explicitly that \(x(0)=0\), \(v(0)=0\), \(v(T)=0\).

addBoundaryConditions( initial = [x = 0,v = 0],
                       final   = [v = 0]);

This is done with the help of a penalty function. There are many types of penalties, they are described more in detail later. For now use a general penalty that works most of the times, the cosine-logarithmic penalty (see Figure XO:logcos and Chapter chap:XO):

addControlBound( u,
                 controlType = "U_COS_LOGARITHMIC",
                 max = 1, min = -2 );

Added the following penalty constraint
  name      = uControl
  class     = PenaltyBarrierU
  u         = u(zeta)
  [min,max] = [-2,1]
  scale     = 1
  epsilon   = .1e-2 (*)
  tolerance = .1e-2 (*)
  type      = U_COS_LOGARITHMIC
  (*) can be changed when using continuation

To have an idea of what this penalty does, consider for simplicity the interval \(I=(a,b)\). Penalty and barrier functions are function that smoothly approximates the characteristic function \(\chi_I(x)\) that is identically zero inside \(I\) and infinity outside \(I\). The problem is that the discontinuity cannot be treated numerically in the convergence process. Hence it is convenient to find a smooth function that approximates the discontinuity.

A barrier function is a smooth functions with takes infinity value outside the interval \(I\), while a penalty function is defined in the whole space while is fastly growing outside the interval \(I\). There are many of those functions available in XOptima, an elegant one is the cosine-logarithmic barrier function. To keep the control in \(I\) and avoid values outside that interval, without limiting the freedom of the solver, the cosine-logarithmic barrier for the interval \(I=[a,b]\) is defined as:

\[ \chi_I(x) \approx p(x) = -c\log\cos\left(\frac{\pi}{2}\cdot\frac{2x-(b+a)}{b-a}\right) \]

with \(c\) such that \(p(x)\) evaluated at \(x=b-\delta\) or \(a+\delta\) takes the value \(\varepsilon\). Where \(\delta=\mathrm{tol}(b-a)/2\) and \(\mathrm{tol}\) is a tolerance and \(\varepsilon\in(0,1)\). The value \(\mathrm{tol}\) is the distance from the border of \(I\) and \(\varepsilon\) is the value assumed by \(p\) at that point. They are therefore useful to control the shape of the function. In particular, notice that inside \(I\) the values of \(p\) are very small, while for \(x\) outside \(I\) the cosine becomes negative, hence the logarithm is complex. The default values are \(\mathrm{tol}=0.001\) and \(\varepsilon=0.001\).

This command will output many informations: the name of the control, by default uControl, the type of the class (penalty, barrier), the control itself \(u(\zeta)\), its range, an eventual scaling factor, the tolerances of the penalty (epsilon and tolerance), the type of the penalty (in this example the cosine-logarithmic). All those quantities are described better later, for this introductory example every parameter is set by default.

To specify the target (that is another name for the functional to be optimised, another used name is performance index) you can choose to write it as a Mayer term or as Lagrange [2] term. You can select both possibilities:

setTarget( lagrange = 0, mayer = -x(zeta_f) );
# or equivalently setTarget( mayer = -x(zeta_f) );

Added target definition
  Lagrange term = -v(zeta)
  Mayer term    = 0

which selects the minimisation of the Mayer term

\[ \min -x(T). \]

To setup the classic Lagrange term

\[ \min \int_0^T -v(t)\dt \]

use the command

setTarget( lagrange = -v(zeta), mayer = 0 );
# or equivalently setTarget( lagrange = -v(zeta) );

Added target definition
  Lagrange term = 0
  Mayer term    = -x(zeta_R)

Please notice the presence of the subscript _f for the final point of the Mayer term. Similarly, for an initial point there is the subscript _i. Although mathematically the two formulations are equivalent, the use of the Lagrange term or the Mayer term will produce (slight) numerical differences.

The setup process is complete, the last thing to do is to tell XOptima to produce the C++ code for the optimal control problem. At this stage you can specify a guess function for the solution, this will improve dramatically the solution process.

The command generateOCProblem is the most important in XOptima because it allows to specify many numerical properties and features (e.g. the use of continuation). In this example it is used in the minimal way. In the next examples more properties will follow. For now consider

generateOCProblem( "Fixed_Time_Bang_Bang",
                   mesh         = [ length=1, n=100 ],
                   states_guess = [ x=0, v=0 ] ) ;

Step 1, generate BVP
--------------------
Generating list of variables
Building penalty functions (Jp_fun)
Building Hamiltonian function (H_fun)
Building gradient of Hamiltonian function (dHdx_vec)
Building dinamical system with co-equation
Building system of equations of optimal controls (g_vec)
Building left and right substitution for jump and boundary conditions
Building equations of boundary conditions (BC_fun, BC_vec)
Building equations for interface or transition conditions

Step 2, solve or guess controls
-------------------------------
       .
       .
       .

Code generation completed!
--------------------------
Deleting unnecessary files!

where

• "Fixed_Time_Bang_Bang" is the name of the project and of the generated C++ object.

• mesh sets the length of the interval for the independent variable and number of nodes

• states_guess for a guess of the states, in this case not very clever as \(x\equiv 0\) and \(v\equiv 0\).

The previous command will generate the C++ and Ruby code to be linked with Mechatronix ToolKit and run with PINS. It is convenient to rewrite the Maple© code for the first example Fixed_Time_Bang_Bang/model/Fixed_Time_BangBang.mw in a unique listing:

# Begin Fixed_Time_Bang_Bang in XOptima
restart:
with(XOptima):
qvars := [x(t),v(t)] ; # commento
cvars := [u(t)] ;
EQ1 := diff(x(t),t) = v(t) ;
EQ2 := diff(v(t),t) = u(t) ;
loadDynamicSystem(equations = [EQ1,EQ2],
                  controls  =  cvars,
                  states    =  qvars) ;
addBoundaryConditions( initial = [x = 0,v = 0],
                       final   = [v = 0]) ;
addControlBound( u,
                 controlType = "U_COS_LOGARITHMIC",
                 max = 1, min = -2 ) ;
setTarget( lagrange = -v(zeta), mayer = 0 ) ;
generateOCProblem( "Fixed_Time_Bang_Bang",
                   mesh         = [ length=1, n=100 ],
                   states_guess = [ x=0, v=0 ] ) ;
# End of Fixed_Time_Bang_Bang in XOptima

Having run the the Maple© sheet, you should find in the Fixed_Time_Bang_Bang folder in the folder tree.

Attention

Folder tree

The folder tree for the first start with PINS after the code generation and the run of the executable.

•   Fixed_Time_Bang_Bang

  •   data

    •   Fixed_Time_Bang_Bang_Data.rb

    •   Fixed_Time_Bang_Bang_OCP_result.txt

  •   lib

    •   Fixed_Time_Bang_Bang_ffi.rb

    •   libFixed_Time_Bang_Bang.[dylib,so,dll]

  •   model

    •   Fixed_Time_Bang_Bang.mw

  •  ocp-cpp

    •   srcs

      •   Fixed_Time_Bang_Bang.cc

      • …

    •   Fixed_Time_Bang_Bang_main.cc

  •   Fixed_Time_Bang_Bang_run.rb

  •   Fixed_Time_Bang_Bang_ruby.rb

To compile and run the code, open a console and surf to the main folder Fixed_Time_Bang_Bang. Then simply type

$ pins Fixed_Time_Bang_Bang_run.rb -f

This will compile, link and run the project, to only run it type

$ pins Fixed_Time_Bang_Bang_run.rb

The final screenshot, after listing of the iterations, will look like

STATISTICS
N. equations  =    407    Iter                  = 14
MaxIter       =    300    tolerance             = 1e-09
lambdaMin     =  1e-20    last residual         = 1.925e-16
lambdaDump    =      2    last ``new'' residual = 1.126e-10
Elapsed Time  =  179.4ms  last ||f||_1          = 1.208e-11


numMeritFunctionEvaluation = 0
numFunctionEvaluation      = 62
numMultiplyByJacobian      = 0
numJacobianFactorization   = 14
numJacobianInversion       = 75
  ______                                          _
 / _____)                                        | |
| /      ___  ____ _   _ ____  ____ ____  ____ _ | |
| |     / _ \|  _ \ | | / _  )/ ___) _  |/ _  ) || |
| \____| |_| | | | \ V ( (/ /| |  ( ( | ( (/ ( (_| |
 \______)___/|_| |_|\_/ \____)_|   \_|| |\____)____|
                                  (_____|
    _     _ _   ____                     _____     _ _          _
   / \   | | | |  _ \  ___  _ __   ___  |  ___|__ | | | __ ___ | |
  / _ \  | | | | | | |/ _ \| '_ \ / _ \ | |_ / _ \| | |/ // __|| |
 / ___ \ | | | | |_| | (_) | | | |  __/ |  _| (_) | |   < \__ \|_|
/_/   \_\|_|_| |____/ \___/|_| |_|\___| |_|  \___/|_|_|\_\|___/(_)

Here you can have some statistics and other informations about the computational time, number of itarations, number of operations in terms of evaluations, inversions etc. The numerical results are stored in a plain text file, called Data/Fixed_Time_Bang_Bang_OCP_result.txt (have a look at folder tree In the results’ files are reported the evaluations of the functions and variables of the OC problem for each node pointwise.

In folder tree is given the typical structure of the directories of the generated files. The first folder Data contains a text file .rb that stores the parameters of the optimal control problem. This is useful if you want to solve several instances of the OCP tuning manually some constants. Modify the Ruby script and you do not have to recompile the C++ project, but simply rerun the executable. In this folder you find also the text file of the results, XOptima will append the string “NOT_CONVERGED” to the file name if the execution of the code does not converge. In the folder lib there are the compiled files of the library with the ffi interface for Ruby: if you are using MS Windows there will be two libraries, a file .lib and a \nfile{.dll}; under Linux a file .a and under OS X a file .dylib. In the directory model there is the source code of your problem in XOptima. The corresponding source code for Mechatronix ToolKit generated and optimised in C++ is contained in the folder ocp-cpp, where you can find the main executable, and in the subfolder srcs there are the header files, the interfaces to C and to Ruby, the source files for the user defined functions. All those files are automatically created by XOptima when you run the command generateOCProblem.

Numerical results

The solution of the classic bang-bang example (1) is \(J^\star=x(T)=\frac{1}{3}\) and

\[ \begin{align*} u(t) &= \begin{cases} 1 & t\in [0,\frac{2}{3})\\[0.5em] -2 & t\in (\frac{2}{3},1] \end{cases} \\[1em] x(t) &= \begin{cases} t^2/2 & t\in [0,\frac{2}{3})\\[0.5em] -t^2+2t-\frac{2}{3} & t\in (\frac{2}{3},1] \end{cases} \\[1em] v(t) &= \begin{cases} t & t\in [0,\frac{2}{3})\\[0.5em] -2t+2 & t\in (\frac{2}{3},1] \end{cases} \\[1em] \lambda_1(t) &=0,\quad \lambda_2(t)=t-\frac{2}{3}. \end{align*} \]

The plot of the results given by PINS is reported in Figure The numerical solution obtained with the code described in Section chap:QS:sec:ex1, with, respectively, the states x and v and the optimal control u..

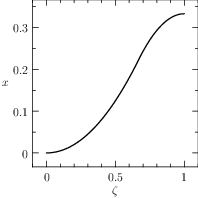
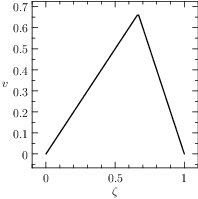
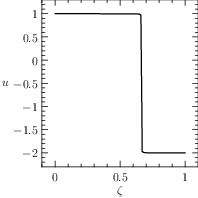
Fig. 5 The numerical solution obtained with the code described in Section Example 1: Fixed Time Bang Bang, with, respectively, the states \(x\) and \(v\) and the optimal control \(u\).

Example 2: Free Time and fixed distance

This second example incrementally introduces a new feature expanding the previous example. The fixed time constraint is removed and a fixed distance to travel is introduced. The OCP is to minimise the time taken to travel from a rest position in the origin to the point at distance \(L=10\). The original mathematical formulation is:

(2)\[\begin{align*} \textrm{minimize: }& T \\[1em] \textrm{ subject to }& x'(t)=v(t), \quad v'(t)=u(t), \qquad t\in[0,T]\\[1em] & x(0)=0, v(0)=0, v(T)=0, x(T)=L; \qquad u(t)\in [-2,1]. \end{align*}\]

To solve a minimum time problem in PINS it is necessary to reformulate it in fixed time, this is done introducing an extra variable, the final time \(T\). The differential equation corresponding to variable \(T\) is obviously \(T'=0\) because the final time is constant. Therefore the problem is defined by three variables \(x\), \(v\), \(T\) and three equations. The independent variable can be set to \(\zeta\) (a kind of time). The original equations of (2) must be multiplied by the factor \(T(\zeta)\) accordingly to the change of variable (for more details on those changes, refer to XO:mintime:

\[ \begin{align*} x'(\zeta) & = T(\zeta)v(\zeta)\\[1em] v'(\zeta) & = T(\zeta)u(\zeta)\\[1em] T'(\zeta) & = 0, \qquad \zeta\in[0,1]. \end{align*} \]

This first part is coded in XOptima in the same way of the previous example and is:

restart:
with(XOptima):
qvars := [x(zeta), v(zeta), T(zeta)];
cvars := [u(zeta)];
EQ1 := diff(x(zeta),zeta) = T(zeta)*v(zeta);
EQ2 := diff(v(zeta),zeta) = T(zeta)*u(t);
EQ2 := diff(T(zeta),zeta) = 0;
loadDynamicSystem( equations = [EQ1,EQ2,EQ3],
                   controls  =  cvars,
                   states    =  qvars );

The boundary conditions are also straightforward to set, also the control does not change:

addBoundaryConditions(initial = [x=0,v=0],final=[v=0,x=L]);
addControlBound( u, controlType="U_COS_LOGARITHMIC",
                 max=1, min=-2, scale = T(zeta) );

Notice that the value \(L\) is defined but not initialised yet. All the parameters and constant are defined together inside the command generateOCProblem at the end of the file.

Warning

serve un commento sulla funzione SCALE

The last part of the script is intuitive and resembles the previous example, it is only matter to define the target, the constants such as the value of \(L=10\) and a guess to help the solver. It is all done with the next two commands

setTarget( lagrange = 0, mayer = T(zeta_f) );
generateOCProblem( "Free_Time_Fixed_Distance",
                   parameters         = [ L = 10 ],
                   mesh               = [ length=1, n=100 ],
                   states_guess       = [ x=L*zeta, v=0, T=1 ],
                   admissible_regions = [ T(zeta)>0 ] );

To solve the problem numerically, it is necessary to specify that the final time \(T\) can not be negative, because clearly a negative time has no physical meaning in this context. This is easily achieved by setting a check on the \(T\) variable with the option admissible_regions.

Again, it is not necessary to conceive a particularly exotic guess, here the three variables are approximated with something reasonable, but it is valuable to point out that a good guess can be effective in the convergence process for complex and structured problems, therefore an at least basic physical knowledge of the problem is important. For conveniency, the complete script for the second example is reported next.

# Begin of Free_Time_Fixed_Distance in XOptima

restart:
with(XOptima):
qvars := [x(zeta), v(zeta), T(zeta)];
cvars := [u(zeta)];
EQ1 := diff(x(zeta),zeta) = T(zeta)*v(zeta);
EQ2 := diff(v(zeta),zeta) = T(zeta)*u(t);
EQ2 := diff(T(zeta),zeta) = 0;
loadDynamicSystem( equations = [EQ1,EQ2,EQ3],
                   controls  =  cvars,
                   states    =  qvars );

addBoundaryConditions(initial = [x=0,v=0],final=[v=0,x=L]);

addControlBound( u, controlType="U_COS_LOGARITHMIC",
                 max=1, min=-2, scale = T(zeta) ) ;

setTarget( lagrange = 0, mayer = T(zeta_f) ) ;

generateOCProblem( "Free_Time_Fixed_Distance",
                   parameters         = [ L = 10 ],
                   mesh               = [ length=1, n=100 ],
                   states_guess       = [ x=L*zeta, v=0, T=1 ],
                   admissible_regions = [ T(zeta)>0 ] ) ;

# End of Free_Time_Fixed_Distance in XOptima

The plot of the results given by PINS is reported in Figure The numerical solution obtained with the code described in Section chap:QS:sec:ex2, with, respectively, the states x and v and the optimal control u..

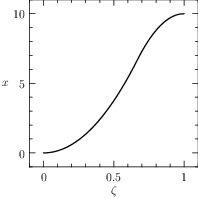
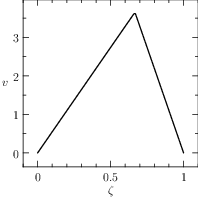
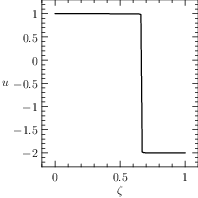
Fig. 6 The numerical solution obtained with the code described in Section Example 2: Free Time and fixed distance, with, respectively, the states \(x\) and \(v\) and the optimal control \(u\).

The exact solution, for a comparison, is quite similar to the previous exercise, the switching point is placed at \(\zeta=\frac{2}{3}\) and the minimum time is \(T^\star=\sqrt{30}\approx 5.47\). The exact solutions of the optimal trajectory and control are:

\[ \begin{align*} u(\zeta) &= \begin{cases} 1 & \zeta\in [0,\frac{2}{3})\\[1em] -2 & \zeta\in (\frac{2}{3},1] \end{cases}\\[1em] x(\zeta) &= \begin{cases} \frac{1}{2}(T\zeta)^2 & \zeta\in [0,\frac{2}{3})\\[1em] -(T\zeta)^2+2\sqrt{30}(T\zeta)-20 & \zeta\in (\frac{2}{3},1] \end{cases}\\[1em] v(\zeta) &= \begin{cases} T\zeta & \zeta\in [0,\frac{2}{3})\\[1em] -2T\zeta+2\sqrt{30} & \zeta\in (\frac{2}{3},1] \end{cases} \end{align*} \]

Example 3: Free Time and fixed distance with two controls

The natural expansion of the previous example is the introduction of two controls, namely the two pedals of the brake \(b(t)\) and of the throttle \(p(t)\), also the fuel mass is taken into account. The controls are antagonists, but it is interesting to see that the optimal solution admits a time interval in which both are saturating. The original problem is a minimum time OCP:

(3)\[\begin{align*} \textrm{minimize:}\quad & T \\[1em] \textrm{subject to:}\quad & x'(t)=v(t), \quad m(t)v'(t)=p(t)-b(t), m'(t)=-k_2p(t); \\[1em] & x(0)=0, v(0)=0, m(0)=m_0, v(T)=0, x(T)=L; \\[1em] & \qquad p(t)\in [0,1],\quad b(t)\in [0,2],\quad t\in[0,T]. \end{align*}\]

The coefficient of fuel consumption is \(k_2=0.2\), the initial mass is \(m_0=1\), the fixed distance to reach is \(L=10\). As seen before, the problem must be firstly converted in a fixed time problem, this is done simply by adding the new (constant) variable \(T\) and the relative change of variable that transforms problem (3) in:

(4)\[\begin{align*} \textrm{minimize:}\quad & T \\[1em] \textrm{subject to:}\quad & x'(\zeta)=T(\zeta)v(\zeta), \quad m(\zeta)v'(\zeta)=T(\zeta)(p(\zeta)-b(\zeta)),\\[1em] & m'(\zeta)=-k_2T(\zeta)p(\zeta), \quad T'(\zeta)=0; \\[1em] & x(0)=0, v(0)=0, m(0)=m_0, v(1)=0, x(1)=L; \\[1em] & \qquad p(\zeta)\in [0,1],\quad b(\zeta)\in [0,2],\quad \zeta\in[0,1]. \end{align*}\]

The plots of the numerical solution of the problem are depicted in Figure The numerical solution obtained with the code described in Section chap:QS:sec:ex3, with, respectively, the states x, v, m and the optimal controls p and b and the optimal time T\approx 4.18..

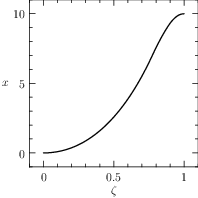
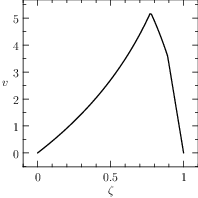
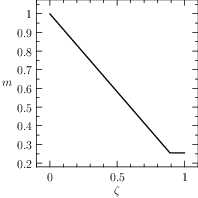
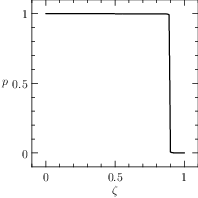
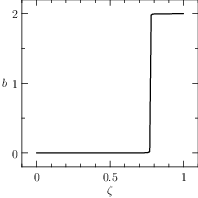
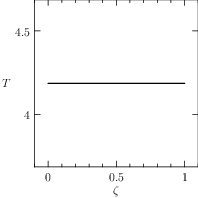
Fig. 7 The numerical solution obtained with the code described in Section Example 3: Free Time and fixed distance with two controls, with, respectively, the states \(x\), \(v\), \(m\) and the optimal controls \(p\) and \(b\) and the optimal time \(T\approx 4.18\).

This is coded directly in XOptima as follows:

# Begin of Free_Time_Fixed_Distance_Two_Controls in XOptima
restart:
with(XOptima):
qvars := [x(zeta), v(zeta), m(zeta), T(zeta)];
cvars := [p(zeta), b(zeta)];
EQ1 := diff(x(zeta),zeta) = T(zeta)*v(zeta);
EQ2 := m(zeta)*diff(v(zeta),zeta) = T(zeta)*(p(zeta)-b(zeta));
EQ3 := diff(m(zeta),zeta) = -T(zeta)*k2*p(zeta);
EQ4 := diff(T(zeta),zeta) = 0;

loadDynamicSystem(equations = [EQ1,EQ2,EQ3,EQ4],
                  controls  =  cvars,
                  states    =  qvars);

addBoundaryConditions(initial = [x=0,v=0,m=m0],final=[v=0,x=L]);

addControlBound( p, controlType="U_COS_LOGARITHMIC",
                 max=1, min=0, scale=T(zeta) ) ;

addControlBound( b, controlType="U_COS_LOGARITHMIC",
                 max=2, min=0, scale=T(zeta) ) ;

setTarget( lagrange = 0, mayer = T(zeta_f) ) ;

generateOCProblem(
  "Free_Time_Mass_Consumption",
  parameters         = [ L = 10, m0=1, k2 = 0.2 ],
  mesh               = [ length=1, n=100 ],
  states_guess       = [ x=L*zeta, v=L, T=1, m = m0 ],
  admissible_regions = [ T(zeta)>0, m(zeta)>0, v(zeta)>=0 ]
);

# End of Free_Time_Fixed_Distance_Two_Controls in XOptima

How to set up an OCP: Quick Start for Experts

Here we show some more advanced features of PINS with classical example from the literature.

Hang Glider

This problem was posed by Bulirsch et al [BNPS91] but consider here the slightly modified version proposed by J.T.Betts in [Bet01]. It requires to maximize the distance \(x(T)\) that a hang glider can travel in presence of a thermal updraft. The difficulty in solving this problem is the sensitivity to the accuracy of the mesh. Both references exploit a combination of direct and indirect methods with some ad hoc tricks in order to obtain convergence of the solver.

The formulation and the constants defined in [Bet01] for the hang glider problem are the following. The dynamical system is

\[ \begin{align*} x'(t) & = v_x(t), \\[0.5em] v'_x(t) & = \dfrac{1}{m}(-L\sin\eta -D\cos \eta) \\[0.5em] y'(t) & = v_y(t), \\[0.5em] v'_y(t) & = \dfrac{1}{m}(L\cos\eta -D\sin \eta-W). \end{align*} \]

The polar drag is \(C_D(C_L)=C_0+kC_L^2\), and the expressions are defined as

(5)\[\begin{align*} D & = \dfrac{1}{2}C_D\rho S v_r^2, \\[0.5em] L & = \dfrac{1}{2}C_L\rho S v_r^2, \\[0.5em] X & = \left(\dfrac{x}{R}-2.5\right)^2, \\[0.5em] u_a(x) & = u_M(1-X)e^{-X}, \\[0.5em] V_y & = v_y-u_a(x), \\[0.5em] v_r & = \sqrt{v_x^2+V_y^2}, \\[0.5em] \sin\eta & = \dfrac{V_y}{v_r}, \\[0.5em] \cos\eta & = \dfrac{v_x}{v_r}. \end{align*}\]

The constants are

\[ \begin{align*} u_M &= 2.5, \\[0.5em] m &= 100\,[kg], \\[0.5em] R &= 100, \\[0.5em] S &= 14 \,[m^2], \\[0.5em] C_0 &= 0.034, \\[0.5em] \rho &= 1.13 \,[kg/m^3], \\[0.5em] k &= 0.069662, \\[0.5em] g &= 9.80665\,[m/s^2], \end{align*} \]

finally \(W=mg\) and the control is the lift coefficient \(C_L\) which is bounded in \(0\leq C_L\leq 1.4\). The boundary conditions for the problem are

\[ \begin{align*} x(0) & = 0, \\[0.5em] x(T) & : \mathrm{free}, \\[0.5em] y(0) & = 1000, \\[0.5em] y(T) & = 900, \\[0.5em] v_x(0) & = 13.2275675, \\[0.5em] v_x(T) & = 13.2275675, \\[0.5em] v_y(0) & = -1.28750052, \\[0.5em] v_y(T) & = -1.28750052. \end{align*} \]

Notice that also the final time \(T\) is free.

The previous equations are coded in XOptima in the usual way:

EQ1  := diff(x(t),t)  = vx(t):
EQ2  := diff(y(t),t)  = vy(t):
EQ3  := diff(vx(t),t) = (-LL*sin_eta-DD*cos_eta)/m:
EQ4  := diff(vy(t),t) = (LL*cos_eta-DD*sin_eta)/m-g:

CD := C0 + k * CL(t)^2;
DD := (1/2) * CD * rho * S * vr^2;
LL := (1/2) * CL(t) * rho * S * vr^2;
Vy := vy(t) - theta*ua(x(t));
vr := sqrt( vx(t)^2 + Vy^2 );
sin_eta := Vy / vr;
cos_eta := vx(t) / vr;

Trying first the pure formulation of Betts without introducing tricks, you cannot achieve (good) convergence to a valid solution. Instead of performing simplifications of the model, it was found out that a new parametrization of the problem in the spatial coordinate, permits to quickly solve the problem in few iterations and little time also on a coarse mesh. Next is given the result of the transform of the problem from time dependence to the spatial variable dependence. The first step is to change from \(t\) to \(x\) the independent variable, this is done via the condition \(x(t(x))=x\) in order to obtain \(t'(x)\) from the equation \(v_x(t(x))t'(x)=1\), whereas for a function \(f(t)\) it holds

\[ \dfrac{\dd f}{\dx}(t(x))=f'(t(x))t'(x) = \dfrac{f'(t(x))}{v_x(x)}. \]

The second step is the change of variable \(x=\zeta \ell(\zeta)\) for the new independent variable \(\zeta\in[0,1]\) and the maximum range \(\ell(\zeta)\) which is constant. Hence, with this choice \(\ell'(\zeta)=0\) and

\[ \dfrac{\dd f}{\dd \zeta}(x(\zeta))=f'(x(\zeta)x'(\zeta)=f'(x(\zeta))\ell(\zeta). \]

The optimal control problem takes the new form of

\[ \begin{align*} t'(\zeta) & = \dfrac{\ell(\zeta)}{v_x(\zeta)}\\[0.5em] y'(\zeta) & = \dfrac{\ell(\zeta)}{v_x(\zeta)}v_y(\zeta)\\[0.5em] v'_x(\zeta) & = \dfrac{\ell(\zeta)}{v_x(\zeta)} \dfrac{\rho S}{2m}v_r(\zeta)\left(-C_D v_x(\zeta)-C_L V_y(\zeta)\right)\\[0.5em] v'_y(\zeta) & = \dfrac{\ell(\zeta)}{v_x(\zeta)}\left[\dfrac{\rho S}{2m}v_r(\zeta)\left(-C_D V_y(\zeta)+C_L v_x(\zeta)\right)-g\right]\\[0.5em] \ell'(\zeta) & = 0, \end{align*} \]

where

\[ v_r(\zeta) = \sqrt{v_x(\zeta)^2+V_y(\zeta)^2}, \qquad V_y(\zeta)=(v_y(\zeta)-u_a(\zeta \ell(\zeta)). \]

The change of coordinates and the reformulation yields the following piece of code:

# change of coordinates
EQX1 := diff(t(x),x)  = 1/vx(x):
EQX2 := diff(y(x),x)  = 1/vx(x)*subs(x(x)=x,subs(t=x,rhs(EQ2))):
EQX3 := diff(vx(x),x) = 1/vx(x)*subs(x(x)=x,subs(t=x,rhs(EQ3))):
EQX4 := diff(vy(x),x) = 1/vx(x)*subs(x(x)=x,subs(t=x,rhs(EQ4))):
<EQX||(1..4)>;

vr := subs(x(x)=x,subs(t=x,vr));

# rescaling the time in [0,1]
SUBS := t(x)  = Time(zeta), y(x)  = y(zeta), vx(x) = vx(zeta),
        vy(x) = vy(zeta),   CL(x) = CL(zeta);
EQXF1:=diff(Time(zeta),zeta)-L(zeta)*subs(SUBS,x=zeta*L(zeta),rhs(EQX1)):
EQXF2:=diff(y(zeta),zeta) -L(zeta)*subs(SUBS,x=zeta*L(zeta),rhs(EQX2)):
EQXF3:=diff(vx(zeta),zeta)-L(zeta)*subs(SUBS,x=zeta*L(zeta),rhs(EQX3)):
EQXF4:=diff(vy(zeta),zeta)-L(zeta)*subs(SUBS,x=zeta*L(zeta),rhs(EQX4)):
EQXF5:=diff(L(zeta),zeta) :

vr := subs(ua(x)=ua(zeta*L(zeta)),x=zeta,vr) ;

The user function \(u_a(x)\) is missing and should be provided by the user. This must be done as an external C++ file, but it has to be declared in XOptima as follows:

addUserFunction(ua(x)) ;

This will tell XOptima and Mechatronix ToolKit that there will be an implementation of \(u_a(x)\). It is not necessary to do it at this moment, the external user function can be setup later. For a better the description of the example how to implement this function is delayed at the end of this section. The final part of the XOptima implementation is described first. At this point the dynamical system is completely specified, it remains only to declare the state and control variables, add the boundary conditions and the options of the command generateOCProblem, for example to setup the continuation.

xvars := [Time(zeta),y(zeta),vx(zeta),vy(zeta),L(zeta)];
uvars := [CL(zeta)];
ode   := [EQXF||(1..5)]:

loadDynamicSystem(equations = ode,
                  controls  = uvars,
                  states    = xvars) ;
addBoundaryConditions(initial = [Time,y,vx,vy],
                      final   = [y,vx,vy]);
addControlBound( CL,
                 controlType="U_COS_LOGARITHMIC",
                 min=0, max=1.4,
                 tolerance = tol_max, epsilon=epsi_max,
                 scale=L(zeta)/L_scale );
addUnilateralConstraint( L(zeta) >0, positiveLen,
                         tolerance = 1, epsilon=0.01 );
setTarget( mayer = -L(zeta_f)/L_scale );

It is convenient, for a better numerical computation, to scale the target so that the numbers are close to 1, hence the presence of the parameter \inlX{L_scale}, that will be set to 1000. Notice the presence of the minus sign in the Mayer term, because the optimisation required is to maximise \(L\). The list of the parameters and the call to the code generator is:

generateOCProblem( "HangGlider",
  post_processing = [[ua(zeta*L(zeta)),"ua"],
                     [vr,"vr"],
                     [zeta*L(zeta),"x"]],
  parameters = [ Time_i = 0,              epsi_min = 0.00001,
                 epsi_max = 0.01,         tol_min  = 0.00001,
                 tol_max  = 0.01,         y_i      = 1000,
                 y_f      = 900,          vx_i     = 13.2275675,
                 vx_f     = 13.2275675,   vy_i     = -1.28750052,
                 vy_f     = -1.28750052,  m        = 100,
                 S        = 14,           C0       = 0.034,
                 rho      = 1.13,         k        = 0.069662,
                 g        = 9.80665,      theta    = 0,
                 L_scale  = 1000 ],
  continuation=[
    [ theta            = s                   ], # step 1
    [ [CL,"epsilon"]   = [epsi_max,epsi_min] ], # step 2
    [ [CL,"tolerance"] = [tol_max,tol_min]   ]  # step 3
  ],

  mesh = [length=1, n=500],
  iterative_controls = [CL=1],
  states_guess       = [Time = zeta*100,
                       y    = y_i+zeta*(y_f-y_i),
                       vx   = vx_i,
                       vy   = vy_i,
                       L    = L_scale ]
);

The constants of the problem are exactly those reported in [Bet01]. The continuation is applied only to the control penalty of \(CL\), the guess are trivial and mostly are linear interpolation of the boundary conditions. In the list of the post processing it is possible to add variables and expression of interest, for example for plotting. To conclude the example it is showed how to setup the user function \(u_a(x)\) as an external C++ file. The file must be placed in a subfolder of the folder model called user-code. The file should be named as the function followed by the suffix “fun”, in this case the filename should be uafun.cc. The user has to specify the function and its first and second derivative. Let’s see how it works for the specific function \(u_a(x)\).

The file uafun.cc has to begin with a standard C++ preamble, such as

#include "HangGlider.hh"

namespace HangGliderDefine {

  using namespace std ;
  using namespace MechatronixCore ;

  static valueType uM = 2.5 ;
  static valueType R  = 100 ;

  valueType HangGlider::ua( valueType x ) const { ... }
  valueType HangGlider::ua_D( valueType x ) const { ... }
  valueType HangGlider::ua_DD( valueType x ) const { ... }
}

The definition of \(u_a(x)\) comes from equations (5), i.e.

\[ X = \left(\dfrac{x}{R}-2.5\right)^2, \qquad u_a(x) = u_M(1-X)e^{-X}, \]

for parameters \(u_M=2.5\) and \(R=100\). This can be appended to the previous code as

valueType
HangGlider::ua( valueType x ) const {
  valueType X = power2(x/R-2.5) ;
  return uM*(1-X)*exp(-X) ;
}

The first and second derivative of \(u_a(x)\) are respectively,

\[ \begin{align*} u_a'(x) &= u_M(X-2)e^{-X}X' \\[0.5em] X' &= \frac{2}{R}(x/R-2.5) \\[0.5em] u_a''(x) &= -(u_M(X-3)e^{-X})X'' \\[0.5em] X'' &= \frac{2}{R^2}. \end{align*} \]

This has to be added to the previous listing (the subscript _D and _DD clearly stays for derivative and second derivative) as

valueType
HangGlider::ua_D( valueType x ) const {
  valueType X   = power2(x/R-2.5) ;
  valueType X_D = (x/R-2.5)*2/R ;
  return (uM*(X-2)*exp(-X))*X_D ;
}

valueType
HangGlider::ua_DD( valueType x ) const {
  valueType X    = power2(x/R-2.5) ;
  valueType X_DD = 2/(R*R) ;
  return -(uM*(X-3)*exp(-X))*X_DD ;
}

You can now generate, compile and run the PINS project Hang Glider. It is enough to write in your console

$ pins HangGlider.rb -f

Start XOptima with a smooth penalty function on the control, that is made sharper at each iteration of the algorithm with the continuation technique. It is obtained a maximum value for \(\ell=x(T)=1248.02\) and a final time \(T=98.43\), with a finer mesh the value was improved to \(1248.030902\), while in [Bet01] is reported a value of \(1248.031026\). The plots for the control and the states are reported in Figure Results for the Hang Glider problem. In the first line: the control C_L, the thermal drift u_a and the position x; in the second line the position y and the velocities v_x and v_y..

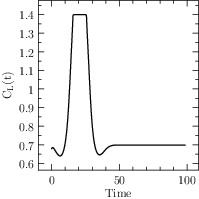
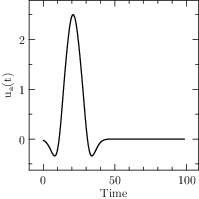
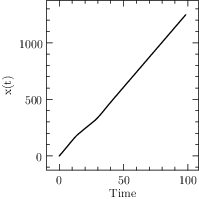
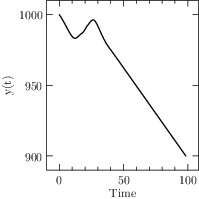
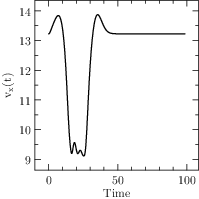
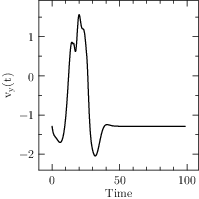
Fig. 8 Results for the Hang Glider problem. In the first line: the control \(C_L\), the thermal drift \(u_a\) and the position \(x\); in the second line the position \(y\) and the velocities \(v_x\) and \(v_y\).

This section ends with the two complete scripts of the XOptima project and the C++ user defined function.

# Begin of Hang Glider in XOptima
EQ1  := diff(x(t),t)  = vx(t):
EQ2  := diff(y(t),t)  = vy(t):
EQ3  := diff(vx(t),t) = (-LL*sin_eta-DD*cos_eta)/m:
EQ4  := diff(vy(t),t) = (LL*cos_eta-DD*sin_eta)/m-g:

CD := C0 + k * CL(t)^2;
DD := (1/2) * CD * rho * S * vr^2;
LL := (1/2) * CL(t) * rho * S * vr^2;
Vy := vy(t) - theta*ua(x(t));
vr := sqrt( vx(t)^2 + Vy^2 );
sin_eta := Vy / vr;
cos_eta := vx(t) / vr;

# change of coordinates
EQX1 := diff(t(x),x)  = 1/vx(x):
EQX2 := diff(y(x),x)  = 1/vx(x)*subs(x(x)=x,subs(t=x,rhs(EQ2))):
EQX3 := diff(vx(x),x) = 1/vx(x)*subs(x(x)=x,subs(t=x,rhs(EQ3))):
EQX4 := diff(vy(x),x) = 1/vx(x)*subs(x(x)=x,subs(t=x,rhs(EQ4))):
<EQX||(1..4)>;

vr := subs(x(x)=x,subs(t=x,vr));

# rescaling the time in [0,1]
SUBS := t(x)  = Time(zeta), y(x)  = y(zeta), vx(x) = vx(zeta),
        vy(x) = vy(zeta),   CL(x) = CL(zeta);
EQXF1:=diff(Time(zeta),zeta)-L(zeta)*subs(SUBS,x=zeta*L(zeta),rhs(EQX1)):
EQXF2:=diff(y(zeta),zeta) -L(zeta)*subs(SUBS,x=zeta*L(zeta),rhs(EQX2)):
EQXF3:=diff(vx(zeta),zeta)-L(zeta)*subs(SUBS,x=zeta*L(zeta),rhs(EQX3)):
EQXF4:=diff(vy(zeta),zeta)-L(zeta)*subs(SUBS,x=zeta*L(zeta),rhs(EQX4)):
EQXF5:=diff(L(zeta),zeta):

vr := subs(ua(x)=ua(zeta*L(zeta)),x=zeta,vr);

addUserFunction(ua(x)) ;

xvars := [Time(zeta),y(zeta),vx(zeta),vy(zeta),L(zeta)];
uvars := [CL(zeta)] ;
ode   := [EQXF||(1..5)] :

loadDynamicSystem(equations = ode,
                  controls  = uvars,
                  states    = xvars) ;
addBoundaryConditions(initial = [Time,y,vx,vy],
                      final   = [y,vx,vy]);
addControlBound( CL,
                 controlType="U_COS_LOGARITHMIC",
                 min=0, max=1.4,
                 tolerance = tol_max, epsilon=epsi_max,
                 scale=L(zeta)/L_scale ) ;
addUnilateralConstraint( L(zeta) >0, positiveLen,
                         tolerance = 1, epsilon=0.01 );
setTarget( mayer = -L(zeta_f)/L_scale );
generateOCProblem( "HangGlider",
  post_processing = [[ua(zeta*L(zeta)),"ua"],
                     [vr,"vr"],
                     [zeta*L(zeta),"x"]],
  parameters = [ Time_i = 0,              epsi_min = 0.00001,
                 epsi_max = 0.01,         tol_min  = 0.00001,
                 tol_max  = 0.01,         y_i      = 1000,
                 y_f      = 900,          vx_i     = 13.2275675,
                 vx_f     = 13.2275675,   vy_i     = -1.28750052,
                 vy_f     = -1.28750052,  m        = 100,
                 S        = 14,           C0       = 0.034,
                 rho      = 1.13,         k        = 0.069662,
                 g        = 9.80665,      theta    = 0,
                 L_scale  = 1000 ],
  continuation=[
    [ theta            = s                   ], # step 1
    [ [CL,"epsilon"]   = [epsi_max,epsi_min] ], # step 2
    [ [CL,"tolerance"] = [tol_max,tol_min]   ]  # step 3
  ],

  mesh = [length=1, n=500],
  iterative_controls = [CL=1],
  states_guess       = [Time = zeta*100,
                        y    = y_i+zeta*(y_f-y_i),
                        vx   = vx_i,
                        vy   = vy_i,
                        L    = L_scale ]
);
# End of Hang Glider in XOptima

//Begin of uafun.cc in C++
#include "HangGlider.hh"

namespace HangGliderDefine {

  using namespace std;
  using namespace MechatronixCore;

  static valueType uM = 2.5;
  static valueType R  = 100;

  valueType
  HangGlider::ua( valueType x ) const {
    valueType X = power2(x/R-2.5);
    return uM*(1-X)*exp(-X);
  }

  valueType
  HangGlider::ua_D( valueType x ) const {
    valueType X   = power2(x/R-2.5);
    valueType X_D = (x/R-2.5)*2/R;
    return (uM*(X-2)*exp(-X))*X_D;
  }

  valueType
  HangGlider::ua_DD( valueType x ) const {
    valueType X    = power2(x/R-2.5);
    valueType X_DD = 2/(R*R);
    return -(uM*(X-3)*exp(-X))*X_DD;
  }

}
//End of uafun.cc in C++

---

[1]

Please notice that XOptima only minimises the functional, in order to maximise it add a minus sign as in (1)

[2]

It is always possible to convert among Mayer problems, Lagrange problems and Bolza problems.