Clip Interval

This is the approximation of the characteristic Clip function, which depends on a certain interval \(I=[a,b]\) and returns \(x\) if \(x\in I\), otherwise the result is \(+1\) if \(x>b\) and \(-1\) if \(x<a\).

Approximation with erf

One approximation is done with the Error Function and is defined in terms of \(h\) and \(\delta\) as (see Figure From left to right the function Clip Interval with the \erf, its first and second derivative.):

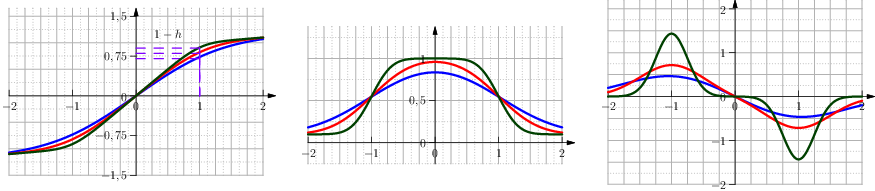
Fig. 15 From left to right the function Clip Interval with the \(\erf\), its first and second derivative.

\[\begin{align*} \mathrm{clip}_{\erf}(x) &\DEF (1-\delta)f(x)+\delta\, x,\\[1em] f(x) & = \frac{1}{2}\left[ (x+1)\erf(\kappa\,(x+1))-(x-1)\erf(\kappa\,(x-1)) + p(x)\right], \end{align*}\]

where

\[ p(x)=\frac{e^{-\kappa^{2}(x+1)^2} -e^{-\kappa^2(x-1)^2}} {\kappa\,\sqrt{\pi}}.\]

The parameter \(\kappa\) is chosen such that \(f(1)=1-h\) therefore

\[ \kappa = \dfrac{1}{2h\sqrt{\pi}}.\]

Approximation with sin(atan())

Another possible approximation is with the help of the trigonometric functions \(\sin\) and \(\arctan\). The Clip function can be regularised in terms of \(h\) and \(\delta\) as (see Figure From left to right the function Clip Interval with SinAtan, its first and second derivative.):

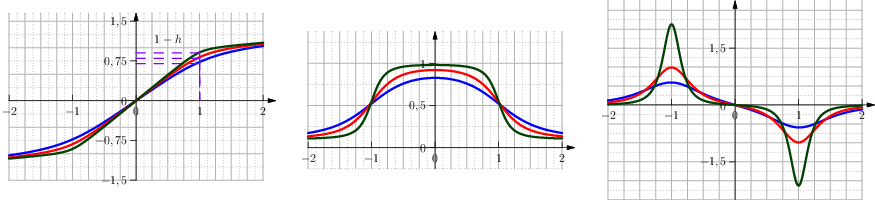
Fig. 16 From left to right the function Clip Interval with SinAtan, its first and second derivative.

\[\begin{align*} \mathrm{clip}_{\textrm{SA}}(x) &\DEF(1-\delta)f(x)+\delta\, x,\\[1em] f(x) & = \frac{2\kappa x}{\sqrt{1+\kappa^2(x+1)^2}+\sqrt{1+\kappa^2(x-1)^2}}. \end{align*}\]

The parameters are set so that \(f(1)=1-h\) and hence

\[ \kappa = \dfrac{1-h}{h(2-h)}.\]

Approximation with polynomials

The polynomial approximation of the Clip function in terms of \(h\) and \(\delta\) takes the form of (see Figure From left to right the function Clip Interval with polynomials, its first and second derivative.):

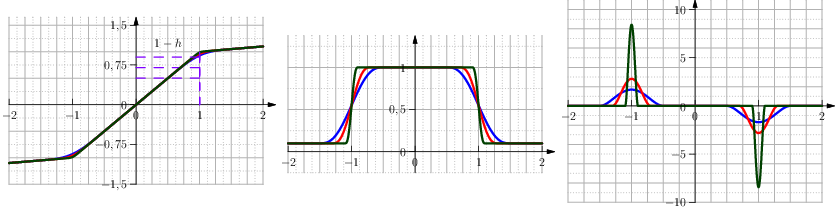
Fig. 17 From left to right the function Clip Interval with polynomials, its first and second derivative.

\[\begin{align*} \mathrm{clip}_{\textrm{poly}}(x) &\DEF (1-\delta)f(x)+\delta\, x,\\[1em] f(x) & = \begin{cases} -1 & x < -1-h \\[0.5em] p(x) & x \in[-1-h,-1+h]\\[0.5em] x & x \in [-1+h,1-h] \\[0.5em] q(x) & x <\in[1-h,1+h] \\[0.5em] 1 & x > 1+h, \end{cases} \end{align*}\]

where

\[\begin{align*} p(x) & = -a+(x+1)(b-(x+1)(c+(x+1)^2(d+e(x+1)^2)))\\[1em] q(x) & = a+(x-1)(b+(x-1)(c+(x-1)^2(d+e(x-1)^2))). \end{align*}\]

The coefficients are

\[a = 1-\frac{5h}{32},\qquad b = \frac{h}{2},\qquad c = -\frac{15h}{32},\qquad d = \frac{5h}{32},\qquad e = -\frac{h}{32}.\]

Clip Rectangle

A function similar to the Clip function is the Clip Rectangle, which is defined as the characteristic function of an interval, i.e. \(\chi_{[0,1]}(x)\) for the interval \([0,1]\). The critical points are smoothed with the regularisation (see Figure From left to right the function Clip Rectangle, its first and second derivative.):

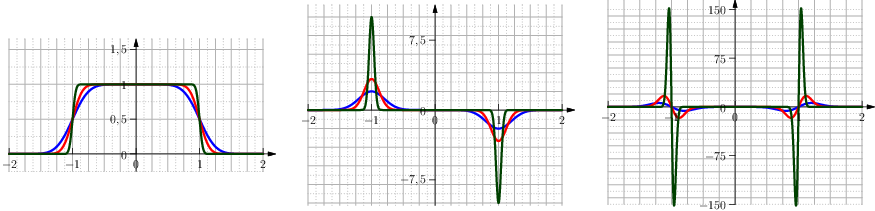
Fig. 18 From left to right the function Clip Rectangle, its first and second derivative.

\[ \mathrm{clip}_{\textrm{R}}(x) \DEF \frac{\erf(\kappa(1-x))+\erf(\kappa(1+x))}{2},\]

so that \(\mathrm{clip}'_{\textrm{R}}(1)=-1/h\). The value of \(\kappa\) is chosen according to the previous requirement, and is computed numerically with an iterative procedure.

Clip Reciprocal

The function Clip Reciprocal (see Figure From left to right the function Clip Reciprocal with its first and second derivative.) is the approximation of the function \(\min(a,1/x)\). The constant \(a\) is given by the user, the parameter \(h\) is the tolerance of:

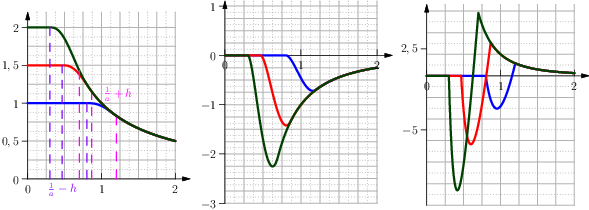
Fig. 19 From left to right the function Clip Reciprocal with its first and second derivative.

\[\mathrm{rec}(x) = \begin{cases} a & \textrm{if $x<1/a-h$} \\[0.5em] a+(x-d)^3(b+c/x) & \textrm{if $x<1/a+h$} \\[0.5em] 1/x & \textrm{otherwise,} \end{cases}\]

with coefficients

\[ b = \frac{a}{16\,h^3}, \qquad c = -\frac{1+3ah}{16\,h^3}, \qquad d = \frac{1}{a}-h.\]

Clip Superior

The function Clip Superior is the approximation of the function \(\min(a,x)\). The constant \(a\) is given by the user, the parameter \(h\) is the tolerance of (see Figure From left to right the function Clip Superior, its first and second derivative.):

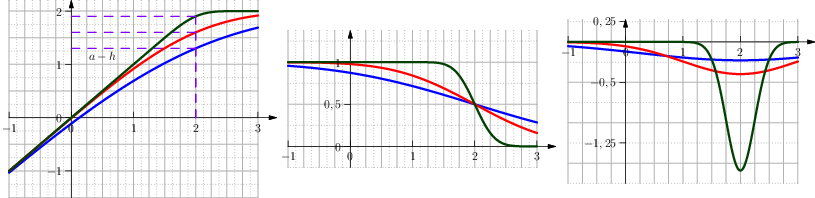
Fig. 20 From left to right the function Clip Superior, its first and second derivative.

\[\mathrm{clip}_{\textrm{sup}}(x) = \frac{x+a}{2} -\frac{x-a}{2}\textrm{erf}(\kappa(x-a)) -\frac{\exp(-\kappa^2(x-a)^2)}{2\kappa\sqrt{\pi}},\]

where \(\kappa\) is {\color{red}chosen to satisfy \(\mathrm{clip}_{\textrm{sup}}(a) =a-h\), and thus} is \(\kappa = \frac{1}{2h\sqrt{\pi}}\).