Regularised 1 norm and distance

The 1-norm of a vector and the distance between two vectors \(\va\) and \(\vb\) in \(\rn\) are given respectively, see Figure fig:XO:norms by

\[ ||\va||_1 \DEF\sum_{i=1}^n|a_i|, \qquad d_1(\va,\vb)\DEF\sum_{i=1}^n|a_i-b_i|.\]

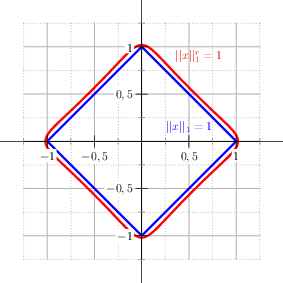
Left: The unitspheres of the three classic norms. Right: comparison with the regularised 1 norm of parameter \(\epsilon=0.2\).

Their regularised counterpart is made such that it is possible to
differentiate the expression and avoid divisions by zero by introducing
a parameter $\epsilon$. The corresponding definitions are

```{math}
  ||\va||_{1,\epsilon}
  \DEF\sum_{i=1}^n \frac{a_i^2}{\sqrt{a_i^2+\epsilon^2}},
  \qquad
  d_{1,\epsilon}(\va,\vb)\DEF\sum_{i=1}^n \frac{(a_i-b_i)^2}{\sqrt{(a_i-b_i)^2+\epsilon^2}}.